
Gauss's inequality
Encyclopedia
In probability theory
, Gauss's inequality (or the Gauss inequality) gives an upper bound on the probability that a unimodal random variable
lies more than any given distance from its mode
.
Let X be a unimodal random variable with mode m, and let τ 2 be the expected value
of (X − m)2. (τ 2 can also be expressed as (μ − m)2 + σ 2, where μ and σ are the mean and standard deviation
of X.) Then for any positive value of k,
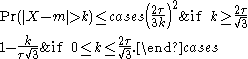
The theorem was first proved by Carl Friedrich Gauss
in 1823.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Gauss's inequality (or the Gauss inequality) gives an upper bound on the probability that a unimodal random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
lies more than any given distance from its mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
.
Let X be a unimodal random variable with mode m, and let τ 2 be the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of (X − m)2. (τ 2 can also be expressed as (μ − m)2 + σ 2, where μ and σ are the mean and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of X.) Then for any positive value of k,
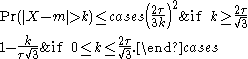
The theorem was first proved by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1823.
See also
- Vysochanskiï–Petunin inequality, a similar result for the distance from the mean rather than the mode
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
, concerns distance from the mean without requiring unimodality

