Feller's coin-tossing constants
Encyclopedia
Feller's coin-tossing constants are a set of numerical constants which describe asymptotic probabilities
that in n independent tosses of a fair coin
, no run of k consecutive heads (or, equally, tails) appears.
William Feller
showed that if this probability is written as p(n,k) then
where αk is the smallest positive real root of
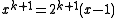
and
For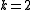
the constants are related to the golden ratio
and Fibonacci numbers; the constants are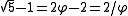
and 
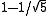. For higher values of 
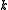they are related to generalizations of Fibonacci numbers
such as the tribonacci and tetranacci constants.
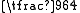= 0.140625. The approximation gives 1.44721356...×1.23606797...−11 = 0.1406263...
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that in n independent tosses of a fair coin
Fair coin
In probability theory and statistics, a sequence of independent Bernoulli trials with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin...
, no run of k consecutive heads (or, equally, tails) appears.
William Feller
William Feller
William Feller born Vilibald Srećko Feller , was a Croatian-American mathematician specializing in probability theory.-Early life and education:...
showed that if this probability is written as p(n,k) then
where αk is the smallest positive real root of
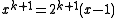
and
Values of the constants
| k |  |  |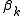
|---|---|---|
| 1 | 2 | 2 |
| 2 | 1.23606797... | 1.44721359... |
| 3 | 1.08737802... | 1.23683983... |
| 4 | 1.03758012... | 1.13268577... |
For
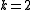the constants are related to the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and Fibonacci numbers; the constants are
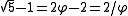and 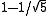. For higher values of 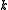they are related to generalizations of Fibonacci numbersGeneralizations of Fibonacci numbers
In mathematics, the Fibonacci numbers form a sequence defined recursively by:The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects...
such as the tribonacci and tetranacci constants.
Example
If we toss a fair coin ten times then the exact probability that no pair of heads come up in succession (i.e. n = 10 and k = 2) is p(10,2) =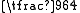 = 0.140625. The approximation gives 1.44721356...×1.23606797...−11 = 0.1406263...