The Eötvös rule, named after the Hungarian physicist Loránd (Roland) Eötvös

Loránd Eötvös

Baron Loránd Eötvös de Vásárosnamény , more commonly called Baron Roland von Eötvös in English literature, was a Hungarian physicist. He is remembered today largely for his work on gravitation and surface tension.-Life:...

 (1848–1919) enables the prediction of the surface tension

Surface tension

Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...

 of an arbitrary liquid

Liquid

Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...

 pure substance at all temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

s. The density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

, molar mass

Molar mass

Molar mass, symbol M, is a physical property of a given substance , namely its mass per amount of substance. The base SI unit for mass is the kilogram and that for amount of substance is the mole. Thus, the derived unit for molar mass is kg/mol...

 and the critical temperature of the liquid have to be known. At the critical point

Critical point (thermodynamics)

In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...

 the surface tension is zero.

The first assumption of the Eötvös rule is:

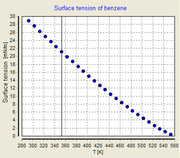
1. The surface tension is a linear function of the temperature.

This assumption is approximately fulfilled for most known liquids. When plotting the surface tension versus the temperature a fairly straight line can be seen which has a surface tension of zero at the critical temperature.

The Eötvös rule also gives a relation of the surface tension behaviour of different liquids in respect to each other:

2. The temperature dependence of the surface tension can be plotted for all liquids in a way that the data collapses to a single master curve. To do so either the molar mass, the density, or the molar volume of the corresponding liquid has to be known.

The Eötvös rule

If V is the molar volume and T_c the critical temperature of a liquid the surface tension

Surface tension

Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...

 γ is given by
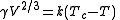
where k is a constant valid for all liquids. The Eötvös constant has a value of 2.1×10⁻⁷ J

Joule

The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...

/(K·mol

Mole (unit)

The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...

^−2/3).

More precise values can be gained when considering that the line normally passes the temperature axis 6 K

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

 before the critical point:


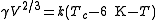
The molar volume V is given by the molar mass M and the density ρ


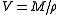
The term 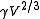is also referred to as the "molar surface tension" γ_mol :

A useful representation that prevents the use of the unit mol^−2/3 is given by the Avogadro constant N_A :

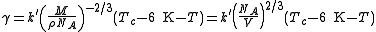
As John Lennard-Jones

John Lennard-Jones

Sir John Edward Lennard-Jones KBE, FRS was a mathematician who was a professor of theoretical physics at Bristol University, and then of theoretical science at Cambridge University...

 and Corner showed in 1940 by means of the statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

 the constant k′ is nearly equal to the Boltzmann constant.

Water

For water, the following equation is valid between 0 and 100 °C.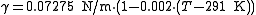

Historical

As student Eötvös started to research surface tension and developed a new method for its determination. The Eötvös rule was first found phenomenological and published in 1886. In 1893 William Ramsay

William Ramsay

Sir William Ramsay was a Scottish chemist who discovered the noble gases and received the Nobel Prize in Chemistry in 1904 "in recognition of his services in the discovery of the inert gaseous elements in air" .-Early years:Ramsay was born in Glasgow on 2...

 and Shields showed an improved version considering that the line normally passes the temperature axis 6 K

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

 before the critical point. John Lennard-Jones

John Lennard-Jones

Sir John Edward Lennard-Jones KBE, FRS was a mathematician who was a professor of theoretical physics at Bristol University, and then of theoretical science at Cambridge University...

 and Corner published (1940) a derivation of the equation by means of statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

. In 1945 E. A. Guggenheim gave a further improved variant of the equation.