
Dudley's theorem
Encyclopedia
In probability theory
, Dudley’s theorem is a result relating the expected
upper bound
and regularity properties
of a Gaussian process
to its entropy
and covariance
structure. The result was proved in a landmark 1967 paper of Richard M. Dudley
; Dudley himself credited Volker Strassen
for making the connection between entropy and regularity.
on T defined by
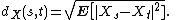
For ε > 0, denote by N(T, dX; ε) the entropy number, i.e. the minimal number of (open) dX-balls of radius ε required to cover T. Then
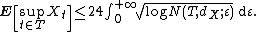
Furthermore, if the entropy integral on the right-hand side converges, then X has a version with almost all sample path bounded and (uniformly) continuous on (T, dX).
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Dudley’s theorem is a result relating the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
and regularity properties
Continuous stochastic process
In the probability theory, a continuous stochastic process is a type of stochastic process that may be said to be "continuous" as a function of its "time" or index parameter. Continuity is a nice property for a process to have, since it implies that they are well-behaved in some sense, and,...
of a Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
to its entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
and covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
structure. The result was proved in a landmark 1967 paper of Richard M. Dudley
Richard M. Dudley
Richard Mansfield Dudley is Professor of Mathematics at the Massachusetts Institute of Technology. He received his PhD at Princeton University in 1962 under the supervision of Edward Nelson and Gilbert Hunt. He was a Putnam Fellow in 1958....
; Dudley himself credited Volker Strassen
Volker Strassen
Volker Strassen is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz.-Biography:Strassen was born on April 29, 1936, in Düsseldorf-Gerresheim....
for making the connection between entropy and regularity.
Statement of the theorem
Let (Xt)t∈T be a Gaussian process and let dX be the pseudometricPseudometric
Pseudometric may refer to:* Pseudo-Riemannian manifold* Pseudometric space...
on T defined by
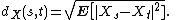
For ε > 0, denote by N(T, dX; ε) the entropy number, i.e. the minimal number of (open) dX-balls of radius ε required to cover T. Then
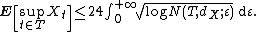
Furthermore, if the entropy integral on the right-hand side converges, then X has a version with almost all sample path bounded and (uniformly) continuous on (T, dX).

