
Dinic's algorithm
Encyclopedia
Dinic's algorithm is a strongly polynomial algorithm for computing the maximum flow in a flow network
, conceived in 1970 by Israeli (formerly Soviet) computer scientist Yefim Dinitz. The algorithm runs in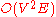 time and is similar to the Edmonds–Karp algorithm, which runs in
time and is similar to the Edmonds–Karp algorithm, which runs in 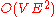 time, in that it uses shortest augmenting paths. The introduction of the concepts of the level graph and blocking flow enable Dinic's algorithm to achieve its performance.
time, in that it uses shortest augmenting paths. The introduction of the concepts of the level graph and blocking flow enable Dinic's algorithm to achieve its performance.
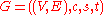 be a network with
be a network with 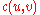 and
and 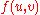 the capacity and the flow of the edge
the capacity and the flow of the edge 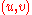 respectively.
respectively.
 blocking flows in the algorithm, where
blocking flows in the algorithm, where  is the number of vertices in the network. The level graph
is the number of vertices in the network. The level graph 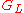 can be constructed by Breadth-first search
can be constructed by Breadth-first search
in time and a blocking flow in each level graph can be found in
time and a blocking flow in each level graph can be found in 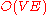 time. Hence, the running time of Dinic's algorithm is
time. Hence, the running time of Dinic's algorithm is 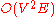 .
.
Using a data structure called dynamic trees, the running time of finding a blocking flow in each phase can be reduced to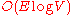 and therefore the running time of Dinic's algorithm can be improved to
and therefore the running time of Dinic's algorithm can be improved to 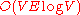 .
.
 time, and it can be shown that the number of phases does not exceed
time, and it can be shown that the number of phases does not exceed 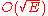 and
and 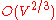 . Thus the algorithm runs in
. Thus the algorithm runs in 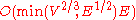 time.
time.
In networks arising during the solution of bipartite matching problem, the number of phases is bounded by , therefore leading to the
, therefore leading to the  time bound. The resulting algorithm is also known as Hopcroft–Karp algorithm. More generally, this bound holds for any unit network — a network in which each vertex, except for source and sink, either has a single entering edge of capacity one, or a single outgoing edge or capacity one, and all other capacities are arbitrary integers.
time bound. The resulting algorithm is also known as Hopcroft–Karp algorithm. More generally, this bound holds for any unit network — a network in which each vertex, except for source and sink, either has a single entering edge of capacity one, or a single outgoing edge or capacity one, and all other capacities are arbitrary integers.
 , the vertices with labels in red are the values
, the vertices with labels in red are the values  . The paths in blue form a blocking flow.
. The paths in blue form a blocking flow.
(Israel), earlier than the Edmonds–Karp algorithm, which was published in 1972 but was discovered earlier. They independently showed that in the Ford–Fulkerson algorithm, if each augmenting path is the shortest one, the length of the augmenting paths is non-decreasing.
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
, conceived in 1970 by Israeli (formerly Soviet) computer scientist Yefim Dinitz. The algorithm runs in
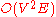 time and is similar to the Edmonds–Karp algorithm, which runs in
time and is similar to the Edmonds–Karp algorithm, which runs in 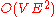 time, in that it uses shortest augmenting paths. The introduction of the concepts of the level graph and blocking flow enable Dinic's algorithm to achieve its performance.
time, in that it uses shortest augmenting paths. The introduction of the concepts of the level graph and blocking flow enable Dinic's algorithm to achieve its performance.Definition
Let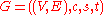 be a network with
be a network with 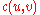 and
and 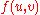 the capacity and the flow of the edge
the capacity and the flow of the edge 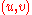 respectively.
respectively.- The residual capacity is a mapping
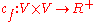 defined as,
defined as,
- if
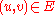 ,
,
-
-
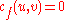 otherwise.
otherwise.
- if
- The residual graph is the graph
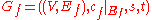 , where
, where
-
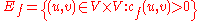 .
.
-
- An augmenting path is an
 path in the residual graph
path in the residual graph  .
.
- Define
 to be the length of the shortest path from
to be the length of the shortest path from  to
to  in
in 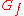 . Then the level graph of
. Then the level graph of 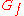 is the graph
is the graph  , where
, where
-
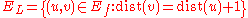 .
.
-
- A blocking flow is an
 flow
flow  such that the graph
such that the graph 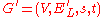 with
with  contains no
contains no  path.
path.
Algorithm
Dinic's Algorithm- Input: A network
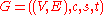 .
. - Output: An
 flow
flow  of maximum value.
of maximum value.
- Set
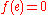 for each
for each  .
. - Construct
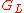 from
from 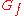 of
of  . If
. If 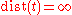 , stop and output
, stop and output  .
. - Find a blocking flow
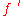 in
in 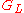 .
. - Augment flow
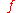 by
by 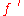 and go back to step 2.
and go back to step 2.
- Set
Analysis
It can be shown that the number of edges in each blocking flow increases by at least 1 each time and thus there are at most blocking flows in the algorithm, where
blocking flows in the algorithm, where  is the number of vertices in the network. The level graph
is the number of vertices in the network. The level graph 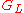 can be constructed by Breadth-first search
can be constructed by Breadth-first searchBreadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
in
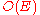 time and a blocking flow in each level graph can be found in
time and a blocking flow in each level graph can be found in 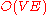 time. Hence, the running time of Dinic's algorithm is
time. Hence, the running time of Dinic's algorithm is 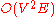 .
.Using a data structure called dynamic trees, the running time of finding a blocking flow in each phase can be reduced to
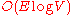 and therefore the running time of Dinic's algorithm can be improved to
and therefore the running time of Dinic's algorithm can be improved to 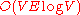 .
.Special cases
In networks with unit capacities, a much stronger time bound holds. Each blocking flow can be found in time, and it can be shown that the number of phases does not exceed
time, and it can be shown that the number of phases does not exceed 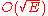 and
and 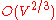 . Thus the algorithm runs in
. Thus the algorithm runs in 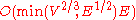 time.
time.In networks arising during the solution of bipartite matching problem, the number of phases is bounded by
 , therefore leading to the
, therefore leading to the  time bound. The resulting algorithm is also known as Hopcroft–Karp algorithm. More generally, this bound holds for any unit network — a network in which each vertex, except for source and sink, either has a single entering edge of capacity one, or a single outgoing edge or capacity one, and all other capacities are arbitrary integers.
time bound. The resulting algorithm is also known as Hopcroft–Karp algorithm. More generally, this bound holds for any unit network — a network in which each vertex, except for source and sink, either has a single entering edge of capacity one, or a single outgoing edge or capacity one, and all other capacities are arbitrary integers.Example
The following is a simulation of the Dinic's algorithm. In the level graph , the vertices with labels in red are the values
, the vertices with labels in red are the values  . The paths in blue form a blocking flow.
. The paths in blue form a blocking flow.  |
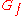 |
 |
|
|---|---|---|---|
| 1. | |||
The blocking flow consists of
Therefore the blocking flow is of 14 units and the value of flow  is 14. Note that each augmenting path in the blocking flow has 3 edges. is 14. Note that each augmenting path in the blocking flow has 3 edges. |
|||
| 2. | |||
The blocking flow consists of
Therefore the blocking flow is of 5 units and the value of flow  is 14 + 5 = 19. Note that each augmenting path has 4 edges. is 14 + 5 = 19. Note that each augmenting path has 4 edges. |
|||
| 3. | |||
Since  cannot be reached in cannot be reached in  . The algorithm terminates and returns a flow with maximum value of 19. Note that in each blocking flow, the number of edges in the augmenting path increases by at least 1. . The algorithm terminates and returns a flow with maximum value of 19. Note that in each blocking flow, the number of edges in the augmenting path increases by at least 1. |
|||
History
Dinic's algorithm was published in 1970 by former Russian Computer Scientist Yefim (Chaim) A. Dinitz , who is today a member of the Computer Science department at Ben-Gurion University of the NegevBen-Gurion University of the Negev
Ben-Gurion University of the Negev is a university in Beersheba, Israel, established in 1969. Ben-Gurion University of the Negev has a current enrollment of 17,400 students, and is one of Israel's fastest growing universities....
(Israel), earlier than the Edmonds–Karp algorithm, which was published in 1972 but was discovered earlier. They independently showed that in the Ford–Fulkerson algorithm, if each augmenting path is the shortest one, the length of the augmenting paths is non-decreasing.



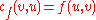
 with 4 units of flow,
with 4 units of flow, with 6 units of flow, and
with 6 units of flow, and with 4 units of flow.
with 4 units of flow. with 5 units of flow.
with 5 units of flow.