
Darboux's theorem
Encyclopedia
Darboux's theorem is a theorem
in the mathematical
field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry. The theorem is named after Jean Gaston Darboux
who established it as the solution of the Pfaff
problem.
One of the many consequences of the theorem is that any two symplectic manifold
s of the same dimension are locally symplectomorphic to one another. That is, every 2n-dimensional symplectic manifold can be made to look locally like the linear symplectic space Cn with its canonical symplectic form. There is also an analogous consequence of the theorem as applied to contact geometry
.
then there is a local system of coordinates x1,...,xn-p, y1, ..., yp in which
If, on the other hand,
then there is a local system of coordinates x1,...,xn-p, y1, ..., yp in which
In particular, suppose that ω is a symplectic 2-form on an n=2m dimensional manifold M. In a neighborhood of each point p of M, by the Poincaré lemma, there is a 1-form θ with dθ=ω. Moreover, θ satisfies the first set of hypotheses in Darboux's theorem, and so locally there is a coordinate chart U near p in which
Taking an exterior derivative
now shows
The chart U is said to be a Darboux chart around p. The manifold M can be covered
by such charts.
To state this differently, identify R2m with Cm by letting zj = xj + i yj. If φ : U → Cn is a Darboux chart, then ω is the pullback of the standard symplectic form ω0 on Cn: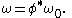
can always be taken, valid near any given point. This is in marked contrast to the situation in Riemannian geometry
where the curvature
is a local invariant, an obstruction to the metric
being locally a sum of squares of coordinate differentials.
The difference is that Darboux's theorem states that ω can be made to take the standard form in an entire neighborhood around p. In Riemannian geometry, the metric can always be made to take the standard form at any given point, but not always in a neighborhood around that point.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in the mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry. The theorem is named after Jean Gaston Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
who established it as the solution of the Pfaff
Johann Friedrich Pfaff
Johann Friedrich Pfaff was a German mathematician. He was described as one of Germany's most eminent mathematicians during the 19th century...
problem.
One of the many consequences of the theorem is that any two symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s of the same dimension are locally symplectomorphic to one another. That is, every 2n-dimensional symplectic manifold can be made to look locally like the linear symplectic space Cn with its canonical symplectic form. There is also an analogous consequence of the theorem as applied to contact geometry
Contact geometry
In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
.
Statement and first consequences
The precise statement is as follows. Suppose that θ is a differential 1-form on an n dimensional manifold, such that dθ has constant rank p. If- θ ∧ (dθ)p = 0 everywhere,
then there is a local system of coordinates x1,...,xn-p, y1, ..., yp in which
- θ = x1 dy1 + ... + xp dyp.
If, on the other hand,
- θ ∧ (dθ)p ≠ 0 everywhere,
then there is a local system of coordinates x1,...,xn-p, y1, ..., yp in which
- θ = x1 dy1 + ... + xp dyp + dxp+1.
In particular, suppose that ω is a symplectic 2-form on an n=2m dimensional manifold M. In a neighborhood of each point p of M, by the Poincaré lemma, there is a 1-form θ with dθ=ω. Moreover, θ satisfies the first set of hypotheses in Darboux's theorem, and so locally there is a coordinate chart U near p in which
- θ = x1 dy1 + ... + xm dym.
Taking an exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
now shows
- ω = dθ = dx1 ∧ dy1 + ... + dxm ∧ dym.
The chart U is said to be a Darboux chart around p. The manifold M can be covered
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
by such charts.
To state this differently, identify R2m with Cm by letting zj = xj + i yj. If φ : U → Cn is a Darboux chart, then ω is the pullback of the standard symplectic form ω0 on Cn:
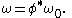
Comparison with Riemannian geometry
This result implies that there are no local invariants in symplectic geometry: a Darboux basisDarboux basis
A Darboux basis may refer either to:* A Darboux basis of a symplectic vector space* In differential geometry, a Darboux frame on a surface.* A Darboux tangent in the dovetail joint....
can always be taken, valid near any given point. This is in marked contrast to the situation in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
where the curvature
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
is a local invariant, an obstruction to the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
being locally a sum of squares of coordinate differentials.
The difference is that Darboux's theorem states that ω can be made to take the standard form in an entire neighborhood around p. In Riemannian geometry, the metric can always be made to take the standard form at any given point, but not always in a neighborhood around that point.

