In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, D’Agostino’s K² test is a goodness-of-fit measure of departure from normality, that is the test aims to establish whether or not the given sample comes from a normally distributed population. The test is based on transformations of the sample kurtosis

Kurtosis

In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...

 and skewness

Skewness

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...

, and has power only against the alternatives that the distribution is skewed and/or kurtic.

Skewness and kurtosis

In the following, let { x_i } denote a sample of n observations, g₁ and g₂ are the sample skewness

Skewness

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...

 and kurtosis

Kurtosis

In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...

, m_j’s are the j-th sample central moment

Central moment

In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...

s, and $\backslash bar\{x\}$ is the sample mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

. (Note that quite frequently in the literature related to normality testing the skewness and kurtosis are denoted as √β₁ and β₂ respectively. Such notation is less convenient since for example √β₁ can be a negative quantity).

The sample skewness and kurtosis are defined as

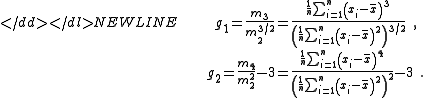
These quantities consistently

Consistent estimator

In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

 estimate the theoretical skewness and kurtosis of the distribution. Moreover, if the sample indeed comes from a normal population, then the exact finite sample distributions of the skewness and kurtosis can themselves be analysed in terms of their means μ₁, variances μ₂, skewnesses γ₁, and kurtoses γ₂. This has been done by , who derived the following expressions:

and

For example, a sample with size drawn from a normally distributed population can be expected to have a skewness of and a kurtosis of , where the ± indicates the standard deviation.

Transformed sample skewness and kurtosis

The sample skewness g₁ and kurtosis g₂ are both asymptotically normal. However the rate of their convergence to the distribution limit is frustratingly slow, especially for g₂. For example even with observations the sample kurtosis g₂ has both the skewness and the kurtosis of approximately 0.3, which is not negligible. In order to remedy this situation, it has been suggested to transform the quantities g₁ and g₂ in a way that makes their distribution as close to standard normal as possible.

In particular, suggested the following transformation for sample skewness:

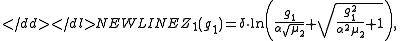
where constants α and δ are computed as

and where μ₂ = μ₂(g₁) is the variance of g₁, and γ₂ = γ₂(g₁) is the kurtosis — the expressions given in the previous section.

Similarly, suggested a transformation for g₂, which works reasonably well for sample sizes of 20 or greater:

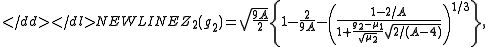
where

and μ₁ = μ₁(g₂), μ₂ = μ₂(g₂), γ₁ = γ₁(g₂) are the quantities computed by Pearson.

Omnibus K² statistic

Statistics Z₁ and Z₂ can be combined to produce an omnibus test, able to detect deviations from normality due to either skewness or kurtosis :

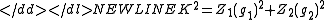
If the null hypothesis

Null hypothesis

The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...

 of normality is true, then K² is approximately χ²-distributed with 2 degrees of freedom.

Note that the statistics g₁, g₂ are not independent, only uncorrelated. Therefore their transforms Z₁, Z₂ will be dependent also , rendering the validity of χ² approximation questionable. Simulations show that under the null hypothesis the K² test statistic is characterized by

	expected value	standard deviation	95% quantile
n = 20	1.971	2.339	6.373
n = 50	2.017	2.308	6.339
n = 100	2.026	2.267	6.271
n = 250	2.012	2.174	6.129
n = 500	2.009	2.113	6.063
n = 1000	2.000	2.062	6.038
χ2(2) distribution	2.000	2.000	5.991

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.