
Conway's Soldiers
Encyclopedia
Conway's Soldiers or the checker-jumping problem is a one-person mathematical game
or puzzle devised and analyzed by mathematician John Horton Conway
in 1961. A variant of peg solitaire
, it takes place on an infinite
checkerboard. The board is divided by a horizontal line that extends indefinitely. Above the line are empty cells and below the line are an arbitrary number of game pieces, or "soldiers". As in peg solitaire, a move consists of one soldier jumping over an adjacent soldier into an empty cell, vertically or horizontally (but not diagonally), and removing the soldier which was jumped over. The goal of the puzzle is to place a soldier as far above the horizontal line as possible.
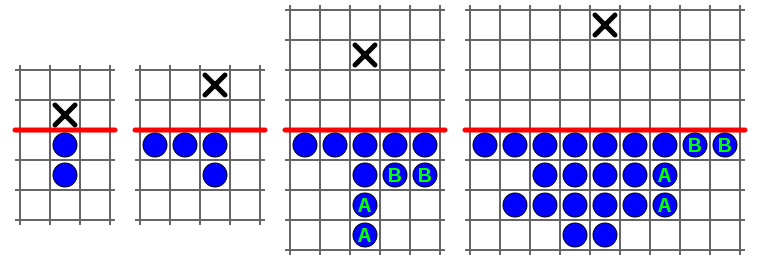
Conway proved that, regardless of the strategy used, there is no finite series of moves that will allow a soldier to advance more than four rows above the horizontal line. His argument uses a carefully chosen weighting of cells (involving the golden ratio
), and he proved that the total weight can only decrease or remain constant. This argument has been reproduced in a number of popular math books.
Simon Tatham
and Gareth Taylor have shown that the fifth row can be reached via an infinite series of moves http://www.chiark.greenend.org.uk/~sgtatham/solarmy/; this result is also in a paper by Pieter Blue and Stephen Hartke http://www.math.unl.edu/~shartke2/. If diagonal jumps are allowed, the 8th row can be reached but not the 9th row. It has also been shown that, in the n-dimensional version of the game, the highest row that can be reached is 3n-2. Conway's weighting argument demonstrates that the row 3n-1 cannot be reached. It is considerably harder to show that row 3n-2 can be reached (see the paper by Eriksson and Lindstrom).
 , and all other squares be labeled
, and all other squares be labeled  , where
, where  is the number of squares away (horizontally and vertically, as in manhattan distance) from the target square. If we consider the starting configuration of soldiers, below the thick red line, we can assign a score based on the sum of the values under each soldier, (e.g.,
is the number of squares away (horizontally and vertically, as in manhattan distance) from the target square. If we consider the starting configuration of soldiers, below the thick red line, we can assign a score based on the sum of the values under each soldier, (e.g.,  etc.) When a soldier jumps over another soldier, there are three cases to consider:
etc.) When a soldier jumps over another soldier, there are three cases to consider:
Choosing a value of
Let us choose a value of  such that the change in score for a positive jump is
such that the change in score for a positive jump is  . Thus, we require
. Thus, we require  = 0 (choosing
= 0 (choosing  gives
gives  which gets us nowhere). Therefore,
which gets us nowhere). Therefore,  , and solving this with the quadratic equation yields
, and solving this with the quadratic equation yields  . We choose the positive root,
. We choose the positive root,  , as its absolute value is less than 1, which becomes useful later in the proof. Rearranging
, as its absolute value is less than 1, which becomes useful later in the proof. Rearranging  , we can see that:
, we can see that:
 [and multiplying by
[and multiplying by  ;]
;]


etc...
Summing this to infinity causes all terms on the right hand side to cancel apart from the 1, i.e.,

This can also be shown with the common ratio, where:


When r =

 . [Drawing a diagram helps to visualise this]. In the next line down, every square is one further away from the target square, and so has value
. [Drawing a diagram helps to visualise this]. In the next line down, every square is one further away from the target square, and so has value  times the square above it, and so on for all the rows below the line.
times the square above it, and so on for all the rows below the line.
Therefore, the total value of all the squares below the line is equal to:
 .
.
At this stage we observe that from above, and thus the above expression simplifies to:
from above, and thus the above expression simplifies to:
 , using
, using  for the last step.
for the last step.
Therefore the sum of all the squares below the line when the target square is immediately above the line is .
.
The next case we consider is when the target square is in the second row above the red line. In this case each square under the red line is one square further away from the target square than in the previous example, so the total score now is found by multiplying the total score we obtained by to give:
to give:
 .
.
Similarly:



Thus, we have shown that when the target square is five rows above the red line, the maximum possible original total score of all the soldiers is 1. In reality, with a finite number of soldiers the total will be less than one. Therefore, since a positive jump towards the target square leaves the total score unaltered, and the final score on all the soldiers must be at least 1 ( and the scores on any other soldiers left), the fifth row cannot be reached with a finite number of soldiers originally below the line.
and the scores on any other soldiers left), the fifth row cannot be reached with a finite number of soldiers originally below the line.
This completes the proof.
 .
.
Mathematical game
A mathematical game is a multiplayer game whose rules, strategies, and outcomes can be studied and explained by mathematics. Examples of such games are Tic-tac-toe and Dots and Boxes, to name a couple. On the surface, a game need not seem mathematical or complicated to still be a mathematical game...
or puzzle devised and analyzed by mathematician John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
in 1961. A variant of peg solitaire
Peg solitaire
Peg solitaire is a board game for one player involving movement of pegs on a board with holes. Some sets use marbles in a board with indentations. The game is known simply as Solitaire in the United Kingdom where the card games are called Patience...
, it takes place on an infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
checkerboard. The board is divided by a horizontal line that extends indefinitely. Above the line are empty cells and below the line are an arbitrary number of game pieces, or "soldiers". As in peg solitaire, a move consists of one soldier jumping over an adjacent soldier into an empty cell, vertically or horizontally (but not diagonally), and removing the soldier which was jumped over. The goal of the puzzle is to place a soldier as far above the horizontal line as possible.

Conway proved that, regardless of the strategy used, there is no finite series of moves that will allow a soldier to advance more than four rows above the horizontal line. His argument uses a carefully chosen weighting of cells (involving the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
), and he proved that the total weight can only decrease or remain constant. This argument has been reproduced in a number of popular math books.
Simon Tatham
Simon Tatham
Simon Tatham is an English programmer known primarily for creating and maintaining PuTTY, a free software implementation of Telnet and SSH clients for Unix and Windows API platforms, along with an xterm terminal emulator...
and Gareth Taylor have shown that the fifth row can be reached via an infinite series of moves http://www.chiark.greenend.org.uk/~sgtatham/solarmy/; this result is also in a paper by Pieter Blue and Stephen Hartke http://www.math.unl.edu/~shartke2/. If diagonal jumps are allowed, the 8th row can be reached but not the 9th row. It has also been shown that, in the n-dimensional version of the game, the highest row that can be reached is 3n-2. Conway's weighting argument demonstrates that the row 3n-1 cannot be reached. It is considerably harder to show that row 3n-2 can be reached (see the paper by Eriksson and Lindstrom).
Notation and definitions
Let the target square be labeled , and all other squares be labeled
, and all other squares be labeled  , where
, where  is the number of squares away (horizontally and vertically, as in manhattan distance) from the target square. If we consider the starting configuration of soldiers, below the thick red line, we can assign a score based on the sum of the values under each soldier, (e.g.,
is the number of squares away (horizontally and vertically, as in manhattan distance) from the target square. If we consider the starting configuration of soldiers, below the thick red line, we can assign a score based on the sum of the values under each soldier, (e.g.,  etc.) When a soldier jumps over another soldier, there are three cases to consider:
etc.) When a soldier jumps over another soldier, there are three cases to consider:- A Positive jump: this is when a soldier jumps towards the target square over another soldier. Let the value of the soldier's square be
 , then the total change in score after a positive jump is
, then the total change in score after a positive jump is  .
. - A Neutral jump; this is when a soldier jumps over another soldier but remains an equal distance from the target square after his jump (should this be necessary). In this case the change in score is -
 .
. - A Negative jump: this is when a soldiers jumps over another into an empty square away from the target square. Here the change in score is
 .
.
Choosing a value of 
Let us choose a value of  such that the change in score for a positive jump is
such that the change in score for a positive jump is  . Thus, we require
. Thus, we require  = 0 (choosing
= 0 (choosing  gives
gives  which gets us nowhere). Therefore,
which gets us nowhere). Therefore,  , and solving this with the quadratic equation yields
, and solving this with the quadratic equation yields  . We choose the positive root,
. We choose the positive root,  , as its absolute value is less than 1, which becomes useful later in the proof. Rearranging
, as its absolute value is less than 1, which becomes useful later in the proof. Rearranging  , we can see that:
, we can see that: [and multiplying by
[and multiplying by  ;]
;]

etc...
Summing this to infinity causes all terms on the right hand side to cancel apart from the 1, i.e.,

This can also be shown with the common ratio, where:


When r =


Solutions
Let us take the first example, where the target square is in the first row above the red line. We now consider the maximum possible initial score, that is when every square has a soldier on it. The sum of the squares on the first row below the red line, is . [Drawing a diagram helps to visualise this]. In the next line down, every square is one further away from the target square, and so has value
. [Drawing a diagram helps to visualise this]. In the next line down, every square is one further away from the target square, and so has value  times the square above it, and so on for all the rows below the line.
times the square above it, and so on for all the rows below the line.Therefore, the total value of all the squares below the line is equal to:
 .
.At this stage we observe that
 from above, and thus the above expression simplifies to:
from above, and thus the above expression simplifies to: , using
, using  for the last step.
for the last step.Therefore the sum of all the squares below the line when the target square is immediately above the line is
 .
.The next case we consider is when the target square is in the second row above the red line. In this case each square under the red line is one square further away from the target square than in the previous example, so the total score now is found by multiplying the total score we obtained by
 to give:
to give: .
.Similarly:



Thus, we have shown that when the target square is five rows above the red line, the maximum possible original total score of all the soldiers is 1. In reality, with a finite number of soldiers the total will be less than one. Therefore, since a positive jump towards the target square leaves the total score unaltered, and the final score on all the soldiers must be at least 1 (
 and the scores on any other soldiers left), the fifth row cannot be reached with a finite number of soldiers originally below the line.
and the scores on any other soldiers left), the fifth row cannot be reached with a finite number of soldiers originally below the line.This completes the proof.
 .
.
