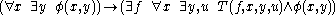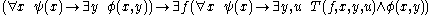Church's thesis (constructive mathematics)
Encyclopedia
In constructive mathematics, Church's thesis is the mathematical assertion that all total functions are recursive
. It gets its name after the informal Church–Turing thesis, which states that every algorithm
is in fact a recursive function
, but the constructivist version is formal and much stronger. It is in fact incompatible with classical logic
.
Where the variables range over the natural number
s, and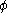 is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel number
is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel number
of a general recursive function which will, for every x, produce such a y satisfying that predicate. (T is some universal predicate which decodes the Gödel-numbering used.)
The thesis is incompatible with classical logic
; adding it to Heyting arithmetic
(HA) allows one to disprove instances of the law of the excluded middle. For instance, it is a classical tautology
that every Turing machine either halts or does not halt on a given input; but if that were true, then from Church's Thesis one would conclude that there is a general recursive function which solves the halting problem
. This is impossible.
However, Heyting arithmetic is equiconsistent with Peano arithmetic (PA) as well as with Heyting arithmetic plus Church's thesis. That is, adding either the law of the excluded middle or Church's thesis can not make Heyting arithmetic inconsistent, but adding both will.
. It can be formally stated by the schema:
In the above,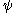 is restricted to be almost-negative. For first-order arithmetic (where the schema is designated
is restricted to be almost-negative. For first-order arithmetic (where the schema is designated 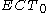 ), this means
), this means  cannot contain any disjunction, and existential quantifiers can only appear in front of
cannot contain any disjunction, and existential quantifiers can only appear in front of 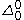 (decidable) formulas.
(decidable) formulas.
This thesis can be characterised as saying that a sentence is true if and only if it is computably realisable. In fact this is captured by the following meta-theoretic equivalences: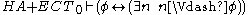
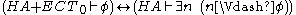
Here,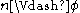 stands for "
stands for "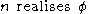 ". So, it is provable in
". So, it is provable in 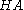 with
with 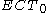 that a sentence is true iff it is realisable. But also,
that a sentence is true iff it is realisable. But also, 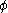 is true in
is true in 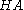 with
with 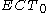 iff
iff 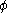 is realisable in
is realisable in  without
without 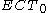 .
.
The second equivalence can be extended with Markov's principle
(M) as follows: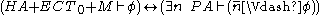
So,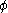 is true in
is true in  with
with 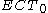 and
and 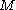 iff there is a number n which realises
iff there is a number n which realises 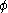 in
in 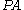 . The existential quantifier has to be outside
. The existential quantifier has to be outside 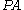 in this case, because PA is non-constructive and lacks the existence property.
in this case, because PA is non-constructive and lacks the existence property.
Recursive function
Recursive function may refer to:*Recursion , a procedure or subroutine, implemented in a programming language, whose implementation references itself*A total computable function, a function which is defined for all possible inputs...
. It gets its name after the informal Church–Turing thesis, which states that every algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is in fact a recursive function
Recursive function
Recursive function may refer to:*Recursion , a procedure or subroutine, implemented in a programming language, whose implementation references itself*A total computable function, a function which is defined for all possible inputs...
, but the constructivist version is formal and much stronger. It is in fact incompatible with classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
.
Formal statement
One way Church's Thesis can be formally stated is by the schema:Where the variables range over the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, and
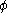 is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel number
is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
of a general recursive function which will, for every x, produce such a y satisfying that predicate. (T is some universal predicate which decodes the Gödel-numbering used.)
The thesis is incompatible with classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
; adding it to Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
(HA) allows one to disprove instances of the law of the excluded middle. For instance, it is a classical tautology
Tautology
Tautology may refer to:*Tautology , using different words to say the same thing even if the repetition does not provide clarity. Tautology also means a series of self-reinforcing statements that cannot be disproved because the statements depend on the assumption that they are already...
that every Turing machine either halts or does not halt on a given input; but if that were true, then from Church's Thesis one would conclude that there is a general recursive function which solves the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
. This is impossible.
However, Heyting arithmetic is equiconsistent with Peano arithmetic (PA) as well as with Heyting arithmetic plus Church's thesis. That is, adding either the law of the excluded middle or Church's thesis can not make Heyting arithmetic inconsistent, but adding both will.
Extended Church's thesis
Extended Church's thesis (ECT) extends the claim to functions which are totally defined over a certain type of domain. It is used by the school of constructive mathematics founded by Andrey Markov JrAndrey Markov (Soviet mathematician)
Andrey Andreyevich Markov Jr. was a Soviet mathematician, the son of the great Russian mathematician Andrey Andreyevich Markov Sr, and one of the key founders of the Russian school of constructive mathematics and logic...
. It can be formally stated by the schema:
In the above,
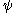 is restricted to be almost-negative. For first-order arithmetic (where the schema is designated
is restricted to be almost-negative. For first-order arithmetic (where the schema is designated 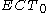 ), this means
), this means  cannot contain any disjunction, and existential quantifiers can only appear in front of
cannot contain any disjunction, and existential quantifiers can only appear in front of 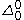 (decidable) formulas.
(decidable) formulas.This thesis can be characterised as saying that a sentence is true if and only if it is computably realisable. In fact this is captured by the following meta-theoretic equivalences:
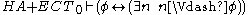
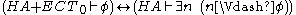
Here,
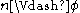 stands for "
stands for "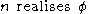 ". So, it is provable in
". So, it is provable in 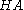 with
with 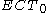 that a sentence is true iff it is realisable. But also,
that a sentence is true iff it is realisable. But also, 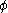 is true in
is true in 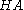 with
with 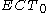 iff
iff 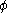 is realisable in
is realisable in  without
without 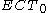 .
.The second equivalence can be extended with Markov's principle
Markov's principle
Markov's principle, named after Andrey Markov Jr, is a classical tautology that is not intuitionistically valid but that may be justified by constructive means.There are many equivalent formulations of Markov's principle.- Statements of the principle :...
(M) as follows:
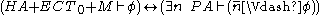
So,
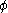 is true in
is true in  with
with 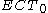 and
and 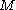 iff there is a number n which realises
iff there is a number n which realises 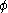 in
in 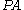 . The existential quantifier has to be outside
. The existential quantifier has to be outside 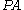 in this case, because PA is non-constructive and lacks the existence property.
in this case, because PA is non-constructive and lacks the existence property.