Bôcher's theorem
Encyclopedia
In mathematics
, Bôcher's theorem can refer to one of two theorems proved by the American mathematician Maxime Bôcher
.
, the theorem states that the finite zeros
of the derivative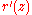
of a nonconstant rational function
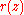that are not multiple zeros are also the positions of equilibrium in the field of force due to particles of positive mass at the zeros of 
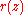and particles of negative mass at the poles of 
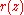, with masses numerically equal to the respective multiplicities, where each particle repels with a force equal to the mass times the inverse distance.
, Bôcher's theorem states that a harmonic function
in punctured domain (an open domain minus one point in the interior) is a linear combination of a harmonic function in the unpunctured domain with a scaled fundamental solution
for the Laplacian in that domain.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Bôcher's theorem can refer to one of two theorems proved by the American mathematician Maxime Bôcher
Maxime Bôcher
Maxime Bôcher was an American mathematician who published about 100 papers on differential equations, series, and algebra. He also wrote elementary texts such as Trigonometry and Analytic Geometry. Bôcher's theorem, Bôcher's equation, and the Bôcher Memorial Prize are named after him.-Life:Bôcher...
.
Bôcher's theorem in complex analysis
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the theorem states that the finite zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of the derivative
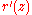of a nonconstant rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
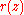that are not multiple zeros are also the positions of equilibrium in the field of force due to particles of positive mass at the zeros of 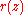and particles of negative mass at the poles of 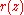, with masses numerically equal to the respective multiplicities, where each particle repels with a force equal to the mass times the inverse distance.Bôcher's theorem for harmonic functions
In harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, Bôcher's theorem states that a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
in punctured domain (an open domain minus one point in the interior) is a linear combination of a harmonic function in the unpunctured domain with a scaled fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
for the Laplacian in that domain.