Borwein's algorithm - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Borwein's algorithm is an algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

devised by Jonathan

Jonathan Borwein

Jonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...

and Peter Borwein

Peter Borwein

Peter Benjamin Borwein is a Canadian mathematicianand a professor at Simon Fraser University. He is known as a co-discoverer of the Bailey-Borwein-Plouffe algorithm for computing π.-First interest in mathematics:...

to calculate the value of 1/π

' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

Jonathan Borwein and Peter Borwein's Version (1993)

Start out by setting

Then

Each additional term of the series yields approximately 50 digits.

Cubic convergence (1991)

Start out by setting

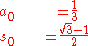
Then iterate

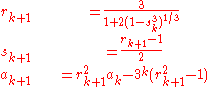
Then a_k converges cubically to 1/π; that is, each iteration approximately triples the number of correct digits.

Another formula for π (1989)

Start out by setting

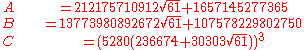
Then

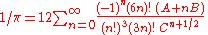
Each additional term of the partial sum yields approximately 31 digits.

Quadratic convergence (1987)

Start out by setting

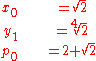
Then iterate

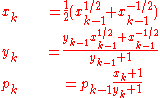
Then p_k converges monotonically to π; with p_k - π ≈ 10^{−2^k+1} for k ≥ 2.s

Borwein's algorithm (1985)

Start out by setting

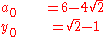
Then iterate

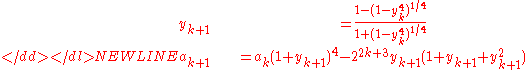
Then a_k converges quartically against 1/π; that is, each iteration approximately quadruples the number of correct digits.

Quartic convergence (1984)

Start out by setting

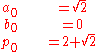
Then iterate

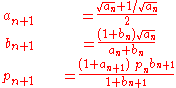
Then p_k converges quartically to π; that is, each iteration approximately quadruples the number of correct digits. The algorithm is not self-correcting; each iteration must be performed with the desired number of correct digits of π.

Quintic convergence

Start out by setting

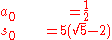
Then iterate

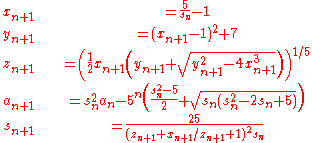
Then a_k converges quintically to 1/π (that is, each iteration approximately quintuples the number of correct digits), and the following condition holds:

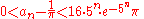
Nonic convergence

Start out by setting

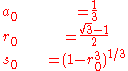
Then iterate

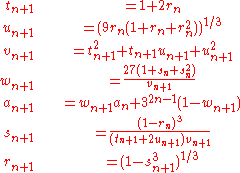
Then a_k converges nonically to 1/π; that is, each iteration approximately multiplies the number of correct digits by nine.

Jonathan Borwein and Peter Borwein's Version (1993)

Cubic convergence (1991)

Another formula for π (1989)

Quadratic convergence (1987)

Borwein's algorithm (1985)

Quartic convergence (1984)

Quintic convergence

Nonic convergence

See also