Blum's speedup theorem
Encyclopedia
In computational complexity theory
Blum's speedup theorem, first stated by Manuel Blum
in 1967, is a fundamental theorem about the complexity of computable function
s.
Each computable function has an infinite number of different program representations in a given programming language. In the theory of algorithms
one often strives to find a program with the smallest complexity for a given computable function and a given complexity measure (such a program could be called optimal). Blum's speedup theorem shows that for any complexity measure there are computable functions which have no optimal program. This also rules out the idea that for any function, one can refer to the computational complexity of this function, meaning the complexity of an optimal program for it.
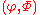and a total computable function 
with two parameters, then there exists a total computable predicate 
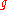(a boolean valued computable function) so that for every program 
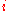for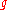 
, there exists a program 
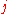for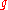 
so that for almost all
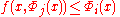
is called the speedup function. The fact that it may be as fast-growing as desired
(as long as it is computable) means that the phenomenon of always having a program of smaller complexity remains even if by "smaller" we mean "significantly smaller" (for instance, quadratically smaller, exponentially smaller).
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
Blum's speedup theorem, first stated by Manuel Blum
Manuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
in 1967, is a fundamental theorem about the complexity of computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s.
Each computable function has an infinite number of different program representations in a given programming language. In the theory of algorithms
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
one often strives to find a program with the smallest complexity for a given computable function and a given complexity measure (such a program could be called optimal). Blum's speedup theorem shows that for any complexity measure there are computable functions which have no optimal program. This also rules out the idea that for any function, one can refer to the computational complexity of this function, meaning the complexity of an optimal program for it.
Speedup theorem
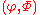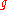Given a Blum complexity measure and a total computable function with two parameters, then there exists a total computable predicate (a boolean valued computable function) so that for every program 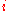for 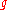, there exists a program 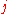for 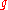so that for almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
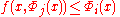
is called the speedup function. The fact that it may be as fast-growing as desired(as long as it is computable) means that the phenomenon of always having a program of smaller complexity remains even if by "smaller" we mean "significantly smaller" (for instance, quadratically smaller, exponentially smaller).