
Bennett's inequality
Encyclopedia
In probability theory
, Bennett's inequality provides an upper bound
on the probability
that the sum of independent random variables deviates from its expected value
by more than any specified amount. Bennett's inequality was proved by George Bennett of the University of New South Wales
in 1962.
Let
be independent random variables, and assume (for simplicity but without loss of generality
) they all have zero expected value. Further assume almost surely
for all , and let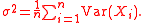
Then for any ,
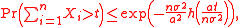
where .
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Bennett's inequality provides an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the sum of independent random variables deviates from its expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
by more than any specified amount. Bennett's inequality was proved by George Bennett of the University of New South Wales
University of New South Wales
The University of New South Wales , is a research-focused university based in Kensington, a suburb in Sydney, New South Wales, Australia...
in 1962.
Let
be independent random variables, and assume (for simplicity but without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
) they all have zero expected value. Further assume almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
for all , and let
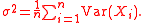
Then for any ,
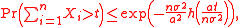
where .

