
Algorithmic Lovász local lemma
Encyclopedia
In theoretical computer science
, the algorithmic Lovász local lemma gives an algorithmic way of constructing objects that obey a system of constraints with limited dependence.
Given a finite set of bad events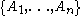 in a probability space with limited dependence amongst the
in a probability space with limited dependence amongst the 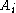 's and with specific bounds on their respective probabilities, the Lovász local lemma
's and with specific bounds on their respective probabilities, the Lovász local lemma
proves that with non-zero probability all of these events can be avoided. However, the lemma is non-constructive in that it does not provide any insight on how to avoid the bad events.
If the events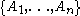 are determined by a finite collection of mutually independent random variables, a simple Las Vegas algorithm
are determined by a finite collection of mutually independent random variables, a simple Las Vegas algorithm
with expected polynomial runtime proposed by Robin Moser and Gábor Tardos
can compute an assignment to the random variables such that all events are avoided.
to prove the existence of certain complex mathematical objects with a set of prescribed features. A typical proof proceeds by operating on the complex object in a random manner and uses the Lovász Local Lemma to bound the probability that any of the features is missing. The absence of a feature is considered a bad event and if it can be shown that all such bad events can be avoided simultaneously with non-zero probability, the existence follows. The lemma itself reads as follows:
Let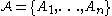 be a finite set of events in the probability space
be a finite set of events in the probability space  . For
. For 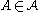 let
let 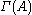 denote a subset of
denote a subset of 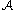 such that
such that 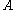 is independent from the collection of events
is independent from the collection of events 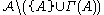 . If there exists an assignment of reals
. If there exists an assignment of reals 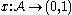 to the events such that
to the events such that

then the probability of avoiding all events in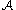 is positive, in particular
is positive, in particular
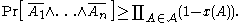
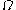 is likely to be inefficient, since the probability of the event of interest
is likely to be inefficient, since the probability of the event of interest  is only bounded by a product of small numbers
is only bounded by a product of small numbers 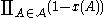 and therefore likely to be very small.
and therefore likely to be very small.
Under the assumption that all of the events in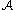 are determined by a finite collection of mutually independent random variables
are determined by a finite collection of mutually independent random variables
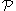 in
in 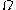 , Robin Moser and Gábor Tardos
, Robin Moser and Gábor Tardos
proposed an efficient randomized algorithm that computes an assignment to the random variables in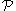 such that all events in
such that all events in 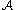 are avoided.
are avoided.
Hence, this algorithm can be used to efficiently construct witnesses of complex objects with prescribed features for most problems to which the Lovász Local Lemma applies.
in 1991 first gave proof that an algorithmic version was possible. In this breakthrough result, a stricter requirement was imposed upon the problem formulation than in the original non-constructive definition. Beck's approach required that for each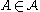 , the number of dependencies of A was bounded above with
, the number of dependencies of A was bounded above with 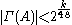 (approximately). The existential version of the Local Lemma permits a larger upper bound on dependencies:
(approximately). The existential version of the Local Lemma permits a larger upper bound on dependencies:
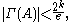
This bound is known to be tight. Since the initial algorithm, work has been done to push algorithmic versions of the Local Lemma closer to this tight value. Moser and Tardos's recent work are the most recent in this chain, and provide an algorithm that achieves this tight bound.
For any random variable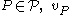 denotes the current assignment (evaluation) of
denotes the current assignment (evaluation) of 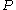 . An assignment (evaluation) to all random variables is denoted
. An assignment (evaluation) to all random variables is denoted 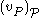 .
.
The unique minimal subset of random variables in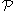 that determine the event
that determine the event 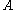 is denoted by
is denoted by 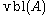 .
.
If the event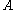 is true under an evaluation
is true under an evaluation 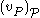 , we say that
, we say that 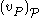 satisfies
satisfies 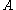 , otherwise it avoids
, otherwise it avoids 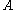 .
.
Given a set of bad events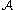 we wish to avoid that is determined by a collection of mutually independent random variables
we wish to avoid that is determined by a collection of mutually independent random variables 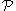 , the algorithm proceeds as follows:
, the algorithm proceeds as follows:
In the first step, the algorithm randomly initializes the current assignment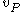 for each random variable
for each random variable 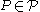 . This means that an assignment
. This means that an assignment 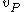 is sampled randomly and independently according to the distribution of the random variable
is sampled randomly and independently according to the distribution of the random variable  .
.
The algorithm then enters the main loop which is executed until all events in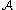 are avoided and which point the algorithm returns the current assignment. At each iteration of the main loop, the algorithm picks an arbitrary satisfied event
are avoided and which point the algorithm returns the current assignment. At each iteration of the main loop, the algorithm picks an arbitrary satisfied event 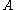 (either randomly or deterministically) and resamples all the random variables that determine
(either randomly or deterministically) and resamples all the random variables that determine 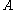 .
.
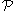 be a finite set of mutually independent random variables in the probability space
be a finite set of mutually independent random variables in the probability space 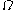 . Let
. Let 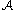 be a finite set of events determined by these variables. If there exists an assignment of reals
be a finite set of events determined by these variables. If there exists an assignment of reals 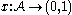 to the events such that
to the events such that
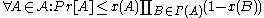
then there exists an assignment of values to the variables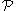 avoiding all of the events in
avoiding all of the events in 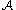 .
.
Moreover, the randomized algorithm described above resamples an event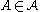 at most an expected
at most an expected  times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most
times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most 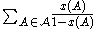 .
.
The proof of this theorem can be found in the paper by Moser and Tardos
 satisfying a set of inequalities in the theorem above is complex and not intuitive. But this requirement can be replaced by three simple conditions:
satisfying a set of inequalities in the theorem above is complex and not intuitive. But this requirement can be replaced by three simple conditions:
The version of the Lovász Local Lemma with these three conditions instead of the assignment function x is called the Symmetric Lovász Local Lemma.
We can also state the Symmetric Algorithmic Lovász Local Lemma:
Let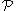 be a finite set of mutually independent random variables and
be a finite set of mutually independent random variables and  be a finite set of events determined by these variables as before. If the above three conditions hold then there exists an assignment of values to the variables
be a finite set of events determined by these variables as before. If the above three conditions hold then there exists an assignment of values to the variables 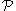 avoiding all of the events in
avoiding all of the events in 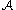 .
.
Moreover, the randomized algorithm described above resamples an event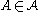 at most an expected
at most an expected 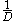 times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most
times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most  .
.
Let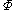 be a CNF
be a CNF
formula over variables , containing
, containing  clauses, and with at least
clauses, and with at least  literals
literals
in each clause, and with each variable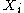 appearing in at most
appearing in at most 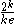 clauses. Then,
clauses. Then, 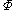 is satisfiable.
is satisfiable.
This statement can be proven easily using the symmetric version of the Algorithmic Lovász Local Lemma. Let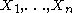 be the set of mutually independent random variables
be the set of mutually independent random variables 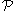 which are sampled uniformly at random.
which are sampled uniformly at random.
Firstly, we truncate each clause in to contain exactly
to contain exactly 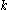 literals. Since each clause is a disjunction, this does not harm satisfiability, for if we can find a satisfying assignment for the truncated formula, it can easily be extended to a satisfying assignment for the original formula by reinserting the truncated literals.
literals. Since each clause is a disjunction, this does not harm satisfiability, for if we can find a satisfying assignment for the truncated formula, it can easily be extended to a satisfying assignment for the original formula by reinserting the truncated literals.
Now, define a bad event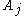 for each clause in
for each clause in 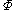 , where
, where 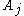 is the event that clause
is the event that clause 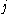 in
in 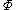 is unsatisfied by the current assignment. Since each clause contains
is unsatisfied by the current assignment. Since each clause contains 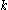 literals (and therefore
literals (and therefore 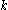 variables) and since all variables are sampled uniformly at random, we can bound the probability of each bad event by
variables) and since all variables are sampled uniformly at random, we can bound the probability of each bad event by 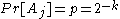 . Since each variable can appear in at most
. Since each variable can appear in at most 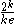 clauses and there are
clauses and there are  variables in each clause, each bad event
variables in each clause, each bad event 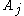 can depend on at most
can depend on at most 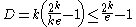 other events.
other events.
Finally, since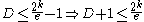 and therefore
and therefore 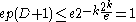 it follows by the symmetric Lovász Local Lemma that the probability of a random assignment to
it follows by the symmetric Lovász Local Lemma that the probability of a random assignment to 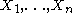 satisfying all clauses in
satisfying all clauses in 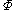 is non-zero and hence such an assignment must exist.
is non-zero and hence such an assignment must exist.
Now, the Algorithmic Lovász Local Lemma actually allows us to efficiently compute such an assignment by applying the algorithm described above. The algorithm proceeds as follows:
It starts with a random truth value assignment to the variables sampled uniformly at random. While there exists a clause in
sampled uniformly at random. While there exists a clause in 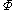 that is unsatisfied, it randomly picks an unsatisfied clause
that is unsatisfied, it randomly picks an unsatisfied clause 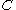 in
in 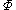 and assigns a new truth value to all variables that appear in
and assigns a new truth value to all variables that appear in 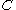 chosen uniformly at random. Once all clauses in
chosen uniformly at random. Once all clauses in 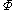 are satisfied, the algorithm returns the current assignment.
are satisfied, the algorithm returns the current assignment.
This algorithm is in fact identical to WalkSAT
which is used to solve general boolean satisfiability problem
s. Hence, the Algorithmic Lovász Local Lemma proves that WalkSAT
has an expected runtime of at most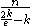 steps on CNF formulas that satisfy the two conditions above.
steps on CNF formulas that satisfy the two conditions above.
A stronger version of the above statement is proven by Moser.
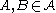 , i.e.
, i.e.  , in parallel is equivalent to resampling
, in parallel is equivalent to resampling 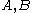 sequentially. Hence, at each iteration of the main loop one can determine the maximal set of independent and satisfied events
sequentially. Hence, at each iteration of the main loop one can determine the maximal set of independent and satisfied events 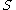 and resample all events in
and resample all events in 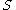 in parallel.
in parallel.
Under the assumption that the assignment function satisfies the slightly stronger conditions:
satisfies the slightly stronger conditions:
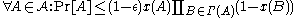
for some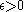 Moser and Tardos proved that the parallel algorithm achieves a better runtime complexity. In this case, the parallel version of the algorithm takes an expected
Moser and Tardos proved that the parallel algorithm achieves a better runtime complexity. In this case, the parallel version of the algorithm takes an expected
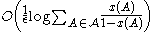
steps before it terminates. The parallel version of the algorithm can be seen as a special case of the sequential algorithm shown above, and so this result also holds for the sequential case.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, the algorithmic Lovász local lemma gives an algorithmic way of constructing objects that obey a system of constraints with limited dependence.
Given a finite set of bad events
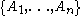 in a probability space with limited dependence amongst the
in a probability space with limited dependence amongst the 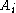 's and with specific bounds on their respective probabilities, the Lovász local lemma
's and with specific bounds on their respective probabilities, the Lovász local lemmaLovász local lemma
In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur...
proves that with non-zero probability all of these events can be avoided. However, the lemma is non-constructive in that it does not provide any insight on how to avoid the bad events.
If the events
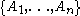 are determined by a finite collection of mutually independent random variables, a simple Las Vegas algorithm
are determined by a finite collection of mutually independent random variables, a simple Las Vegas algorithmLas Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
with expected polynomial runtime proposed by Robin Moser and Gábor Tardos
Gábor Tardos
Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...
can compute an assignment to the random variables such that all events are avoided.
Review of Lovász local lemma
The Lovász Local Lemma is a powerful tool commonly used in the probabilistic methodProbabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
to prove the existence of certain complex mathematical objects with a set of prescribed features. A typical proof proceeds by operating on the complex object in a random manner and uses the Lovász Local Lemma to bound the probability that any of the features is missing. The absence of a feature is considered a bad event and if it can be shown that all such bad events can be avoided simultaneously with non-zero probability, the existence follows. The lemma itself reads as follows:
Let
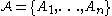 be a finite set of events in the probability space
be a finite set of events in the probability space  . For
. For 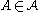 let
let 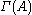 denote a subset of
denote a subset of 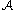 such that
such that 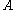 is independent from the collection of events
is independent from the collection of events 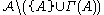 . If there exists an assignment of reals
. If there exists an assignment of reals 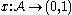 to the events such that
to the events such that
then the probability of avoiding all events in
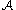 is positive, in particular
is positive, in particular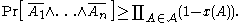
Algorithmic version of the Lovász local lemma
The Lovász Local Lemma is non-constructive because it only allows us to conclude the existence of structural properties or complex objects but does not indicate how these can be found or constructed efficiently in practice. Note that random sampling from the probability space is likely to be inefficient, since the probability of the event of interest
is likely to be inefficient, since the probability of the event of interest  is only bounded by a product of small numbers
is only bounded by a product of small numbers 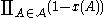 and therefore likely to be very small.
and therefore likely to be very small.Under the assumption that all of the events in
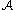 are determined by a finite collection of mutually independent random variables
are determined by a finite collection of mutually independent random variablesRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
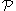 in
in 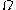 , Robin Moser and Gábor Tardos
, Robin Moser and Gábor TardosGábor Tardos
Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...
proposed an efficient randomized algorithm that computes an assignment to the random variables in
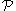 such that all events in
such that all events in 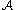 are avoided.
are avoided.Hence, this algorithm can be used to efficiently construct witnesses of complex objects with prescribed features for most problems to which the Lovász Local Lemma applies.
History
Prior to the recent work of Moser and Tardos, earlier work had also made progress in developing algorithmic versions of the Lovász Local Lemma. József BeckJózsef Beck
József Beck is a Harold H. Martin Professor of Mathematics at Rutgers University.His contributions to combinatorics include the partial colouring lemma and the Beck–Fiala theorem in discrepancy theory, the algorithmic version of the Lovász local lemma, the two extremes theorem in combinatorial...
in 1991 first gave proof that an algorithmic version was possible. In this breakthrough result, a stricter requirement was imposed upon the problem formulation than in the original non-constructive definition. Beck's approach required that for each
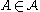 , the number of dependencies of A was bounded above with
, the number of dependencies of A was bounded above with 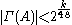 (approximately). The existential version of the Local Lemma permits a larger upper bound on dependencies:
(approximately). The existential version of the Local Lemma permits a larger upper bound on dependencies: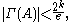
This bound is known to be tight. Since the initial algorithm, work has been done to push algorithmic versions of the Local Lemma closer to this tight value. Moser and Tardos's recent work are the most recent in this chain, and provide an algorithm that achieves this tight bound.
Algorithm
Let us first introduce some concepts that are used in the algorithm.For any random variable
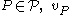 denotes the current assignment (evaluation) of
denotes the current assignment (evaluation) of 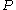 . An assignment (evaluation) to all random variables is denoted
. An assignment (evaluation) to all random variables is denoted 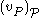 .
.The unique minimal subset of random variables in
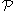 that determine the event
that determine the event 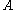 is denoted by
is denoted by 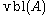 .
.If the event
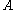 is true under an evaluation
is true under an evaluation 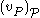 , we say that
, we say that 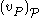 satisfies
satisfies 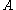 , otherwise it avoids
, otherwise it avoids 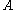 .
.Given a set of bad events
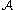 we wish to avoid that is determined by a collection of mutually independent random variables
we wish to avoid that is determined by a collection of mutually independent random variables 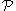 , the algorithm proceeds as follows:
, the algorithm proceeds as follows:-
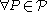 :
:  a random evaluation of P
a random evaluation of P - while
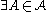 such that A is satisfied by
such that A is satisfied by 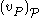
- pick an arbitrary satisfied event

-
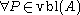 :
: 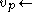 a new random evaluation of P
a new random evaluation of P
- pick an arbitrary satisfied event
- return
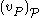
In the first step, the algorithm randomly initializes the current assignment
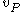 for each random variable
for each random variable 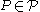 . This means that an assignment
. This means that an assignment 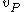 is sampled randomly and independently according to the distribution of the random variable
is sampled randomly and independently according to the distribution of the random variable  .
.The algorithm then enters the main loop which is executed until all events in
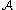 are avoided and which point the algorithm returns the current assignment. At each iteration of the main loop, the algorithm picks an arbitrary satisfied event
are avoided and which point the algorithm returns the current assignment. At each iteration of the main loop, the algorithm picks an arbitrary satisfied event 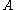 (either randomly or deterministically) and resamples all the random variables that determine
(either randomly or deterministically) and resamples all the random variables that determine 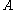 .
.Main theorem
Let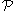 be a finite set of mutually independent random variables in the probability space
be a finite set of mutually independent random variables in the probability space 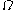 . Let
. Let 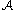 be a finite set of events determined by these variables. If there exists an assignment of reals
be a finite set of events determined by these variables. If there exists an assignment of reals 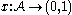 to the events such that
to the events such that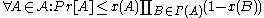
then there exists an assignment of values to the variables
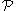 avoiding all of the events in
avoiding all of the events in 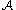 .
.Moreover, the randomized algorithm described above resamples an event
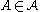 at most an expected
at most an expected  times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most
times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most 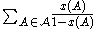 .
.The proof of this theorem can be found in the paper by Moser and Tardos
Symmetric version
The requirement of an assignment function satisfying a set of inequalities in the theorem above is complex and not intuitive. But this requirement can be replaced by three simple conditions:
satisfying a set of inequalities in the theorem above is complex and not intuitive. But this requirement can be replaced by three simple conditions:
-
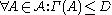 , i.e. each event
, i.e. each event 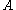 depends on at most
depends on at most  other events,
other events, -
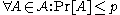 , i.e. the probability of each event
, i.e. the probability of each event  is at most
is at most 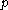 ,
, -
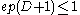 , where
, where  is the base of the natural logarithmE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
is the base of the natural logarithmE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
.
The version of the Lovász Local Lemma with these three conditions instead of the assignment function x is called the Symmetric Lovász Local Lemma.
We can also state the Symmetric Algorithmic Lovász Local Lemma:
Let
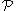 be a finite set of mutually independent random variables and
be a finite set of mutually independent random variables and  be a finite set of events determined by these variables as before. If the above three conditions hold then there exists an assignment of values to the variables
be a finite set of events determined by these variables as before. If the above three conditions hold then there exists an assignment of values to the variables 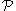 avoiding all of the events in
avoiding all of the events in 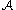 .
.Moreover, the randomized algorithm described above resamples an event
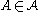 at most an expected
at most an expected 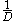 times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most
times before it finds such an evaluation. Thus the expected total number of resampling steps and therefore the expected runtime of the algorithm is at most  .
.Example
The following example illustrates how the algorithmic version of the Lovász Local Lemma can be applied to a simple problem.Let
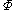 be a CNF
be a CNFConjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
formula over variables
 , containing
, containing  clauses, and with at least
clauses, and with at least  literals
literalsLiteral (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
in each clause, and with each variable
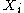 appearing in at most
appearing in at most 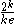 clauses. Then,
clauses. Then, 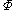 is satisfiable.
is satisfiable.This statement can be proven easily using the symmetric version of the Algorithmic Lovász Local Lemma. Let
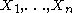 be the set of mutually independent random variables
be the set of mutually independent random variables 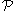 which are sampled uniformly at random.
which are sampled uniformly at random.Firstly, we truncate each clause in
 to contain exactly
to contain exactly 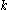 literals. Since each clause is a disjunction, this does not harm satisfiability, for if we can find a satisfying assignment for the truncated formula, it can easily be extended to a satisfying assignment for the original formula by reinserting the truncated literals.
literals. Since each clause is a disjunction, this does not harm satisfiability, for if we can find a satisfying assignment for the truncated formula, it can easily be extended to a satisfying assignment for the original formula by reinserting the truncated literals.Now, define a bad event
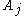 for each clause in
for each clause in 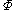 , where
, where 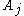 is the event that clause
is the event that clause 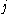 in
in 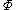 is unsatisfied by the current assignment. Since each clause contains
is unsatisfied by the current assignment. Since each clause contains 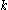 literals (and therefore
literals (and therefore 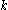 variables) and since all variables are sampled uniformly at random, we can bound the probability of each bad event by
variables) and since all variables are sampled uniformly at random, we can bound the probability of each bad event by 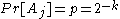 . Since each variable can appear in at most
. Since each variable can appear in at most 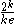 clauses and there are
clauses and there are  variables in each clause, each bad event
variables in each clause, each bad event 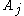 can depend on at most
can depend on at most 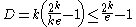 other events.
other events.Finally, since
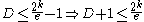 and therefore
and therefore 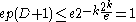 it follows by the symmetric Lovász Local Lemma that the probability of a random assignment to
it follows by the symmetric Lovász Local Lemma that the probability of a random assignment to 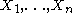 satisfying all clauses in
satisfying all clauses in 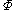 is non-zero and hence such an assignment must exist.
is non-zero and hence such an assignment must exist.Now, the Algorithmic Lovász Local Lemma actually allows us to efficiently compute such an assignment by applying the algorithm described above. The algorithm proceeds as follows:
It starts with a random truth value assignment to the variables
 sampled uniformly at random. While there exists a clause in
sampled uniformly at random. While there exists a clause in 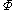 that is unsatisfied, it randomly picks an unsatisfied clause
that is unsatisfied, it randomly picks an unsatisfied clause 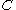 in
in 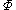 and assigns a new truth value to all variables that appear in
and assigns a new truth value to all variables that appear in 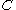 chosen uniformly at random. Once all clauses in
chosen uniformly at random. Once all clauses in 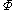 are satisfied, the algorithm returns the current assignment.
are satisfied, the algorithm returns the current assignment.This algorithm is in fact identical to WalkSAT
WalkSAT
GSAT and WalkSat are local search algorithms to solve Boolean satisfiability problems.Both algorithms work on formulae that are in, or have been converted into, conjunctive normal form. They start by assigning a random value to each variable. If the assignment satisfies all clauses, the algorithm...
which is used to solve general boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
s. Hence, the Algorithmic Lovász Local Lemma proves that WalkSAT
WalkSAT
GSAT and WalkSat are local search algorithms to solve Boolean satisfiability problems.Both algorithms work on formulae that are in, or have been converted into, conjunctive normal form. They start by assigning a random value to each variable. If the assignment satisfies all clauses, the algorithm...
has an expected runtime of at most
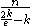 steps on CNF formulas that satisfy the two conditions above.
steps on CNF formulas that satisfy the two conditions above.A stronger version of the above statement is proven by Moser.
Applications
As mentioned before, the Algorithmic Version of the Lovász Local Lemma applies to most problems for which the general Lovász Local Lemma is used as a proof technique. Some of these problems are discussed in the following articles:- Probabilistic proofs of non-probabilistic theoremsProbabilistic proofs of non-probabilistic theoremsProbability theory routinely uses results from other fields of mathematics . The opposite cases, collected below, are relatively rare; however, probability theory is used systematically in combinatorics via the probabilistic method. They are particularly used for non-constructive proofs.-Analysis:*...
- Random graphRandom graphIn mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
Parallel version
The algorithm described above lends itself well to parallelization, since resampling two independent events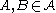 , i.e.
, i.e.  , in parallel is equivalent to resampling
, in parallel is equivalent to resampling 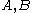 sequentially. Hence, at each iteration of the main loop one can determine the maximal set of independent and satisfied events
sequentially. Hence, at each iteration of the main loop one can determine the maximal set of independent and satisfied events 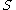 and resample all events in
and resample all events in 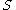 in parallel.
in parallel.Under the assumption that the assignment function
 satisfies the slightly stronger conditions:
satisfies the slightly stronger conditions: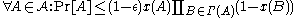
for some
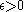 Moser and Tardos proved that the parallel algorithm achieves a better runtime complexity. In this case, the parallel version of the algorithm takes an expected
Moser and Tardos proved that the parallel algorithm achieves a better runtime complexity. In this case, the parallel version of the algorithm takes an expected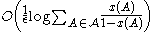
steps before it terminates. The parallel version of the algorithm can be seen as a special case of the sequential algorithm shown above, and so this result also holds for the sequential case.

